

The slope of the line is the rate of change, and the y-intercept is the point where the line crosses the y-axis. The equation of a linear trendline is y=mx+b, where y is the dependent variable, m is the slope of the line, x is the independent variable, and b is the y-intercept. You can use the equation of the trendline to make predictions about future data points. Excel will automatically calculate the trendline and add it to your graph. To add a linear trendline to your data, select the "Linear" option from the trendline menu. They are best used with linear data, which is data that increases or decreases at a constant rate. Linear trendlines are the simplest type of trendline. Select the type of trendline you want to use. A menu will appear with different types of trendlines you can add to your data. Then, click the "Insert" tab on the ribbon and click the "Trendline" button. To add a trendline to your Excel graph, first select the data you want to use to create the trendline. In this article, well show you how to add a trendline to your Excel graph and interpret the results. Trendlines are best used with linear data, but you can also add them to logarithmic, polynomial, and exponential data. I have learnt things I didn't know previously.Adding a trendline to your Excel graph can help you see patterns in your data and make predictions about future data points. At the same time I can see how increasing the number of decimal places at least in some cases gives better results. So in summary, I am at a loss to understand why the equations in the first worksheet were wrong, yet in a new worksheet using the same table of data the equations were okay. The equation became y = 0.000640x^2 - 0.144000x + 10.400000 and now all 3 original and 4 extra values of x gave very good agreement, as was the case with the first chart. So for the second chart I increased the equation to 6 decimal places. Nor did the other 4 points exactly match the trendline. When I tested the formula (with 2 decimal places) the values didn't match exactly the 3 original values of y. In the case of the second chart the equation had changed from y = 0.68x^2 + 2.05x + 99.75 to y = 0.00x^2 - 0.14x + 10.40. All this with a setting of 2 decimal places. I tried another 4 values of x and all gave y values that appear to match the trendline.
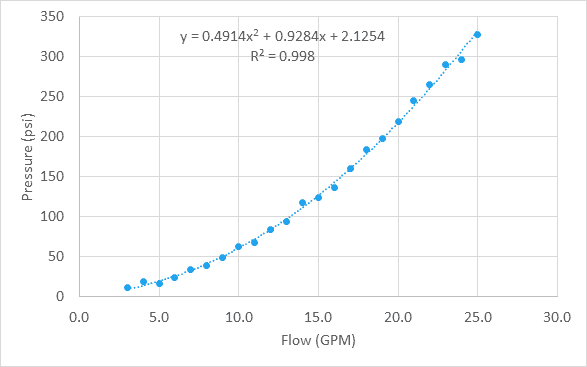
I then used the new equation with the 3 original x values and all got exactly the correct y values. Amazingly, at least to me, while the 3 points for each chart were unchanged, the equations changed radically. Since my last post I have created a new worksheet and recreated the 2 charts and then added trendlines and equations.


 0 kommentar(er)
0 kommentar(er)
